En general, las comunicaciones seguras deberían formar parte del conjunto de soluciones de ciberseguridad, no del problema. Cuando la CVE-2022-0778 reveló que un certificado SSL malintencionado podía conducir a una utilización casi total de la CPU y a una denegación de servicio en una máquina objetivo, pensamos que sería instructivo ver exactamente cómo algo tan positivo puede, en situaciones muy específicas, salir tan mal.
CVE-2022-0778 en pocas palabras
OpenSSL es una biblioteca muy popular, ampliamente utilizada por muchas organizaciones y aplicaciones de software que requieren comunicaciones seguras. Una vulnerabilidad de OpenSSL recientemente revelada, CVE-2022-0778, puede utilizar certificados especialmente manipulados para provocar una denegación de servicio (DoS). La vulnerabilidad afecta tanto a los clientes como a los servidores.
La vulnerabilidad radica en la implementación de OpenSSL del algoritmo Tonelli-Shanks, utilizado para encontrar las raíces cuadradas de los números en la criptografía de curva elíptica que constituye el núcleo de la biblioteca de cifrado. Esta vulnerabilidad se produce cuando en lugar de un número primo, se pasa al algoritmo, un número compuesto. Esto resulta en un problema computacional como factorización de enteros.
En este informe explicaremos primero los fundamentos de la criptografía de curva elíptica, y luego proporcionaremos un análisis detallado del problema que conduce a la CVE-2022-0778. Se trata de una matemática interesante, por lo que la analizaremos cuidadosamente.
Criptografía de curva elíptica
La criptografía de curva elíptica (ECC) es una criptografía de clave pública basada en curvas elípticas. Es un sucesor moderno del legendario criptosistema RSA, pero utilizando las interesantes propiedades de las curvas elípticas en lugar de la multiplicación de números primos de RSA. Como ECC puede utilizar claves de menor tamaño, es más rápido que RSA, una ventaja evidente.
Las curvas elípticas son curvas algebraicas. La siguiente ecuación describe una curva elíptica:
Ax3 + Bx2 y + Cxy2 + Dy3 + Ex2 + Fxy + Gy2 + Hx + Iy +J = 0
Aquí A,B…J definen la curva. Sin embargo, en criptografía se utiliza una forma simplificada de la ecuación, denominada función elíptica de Weierstrass:
y2 = x3 + ax + b
Si visualizamos la curva, vemos algo así:
Si tomamos dos puntos de esta curva -el punto 1 y el punto 2- y trazamos una línea, esa línea corta la curva en el punto 3. Si tomamos el punto opuesto (es decir, el punto igual al punto 3, en el otro lado del eje X), será el punto 1 + punto2, como se muestra en la imagen anterior.
ECC utiliza una curva elíptica sobre campos finitos, y los puntos de la curva están limitados a coordenadas enteras. Por lo tanto, la curva anterior en la forma modular será como sigue
y2 ≡ x3 + ax + b (mod p)
Donde p es un número primo que denota el tamaño del campo. (El símbolo ≡ denota congruencia).
En segundo lugar, las curvas elípticas se definen sobre campos finitos. Por ello, existe para cada curva elíptica un punto constante predefinido, que se denomina G – el punto generador, también conocido como punto base. Cualquier punto P en el subgrupo sobre la curva elíptica puede generarse multiplicando G por algún número entero, K, así
P = K*G
Finalmente, realizar la ecuación algebraica en dos puntos cualquiera del campo, dará como resultado otro punto en el mismo. Todos los puntos de la curva elíptica sobre un campo finito forman un grupo finito; el número total de puntos se llama el orden de la curva y se denota por n. Puede haber múltiples subgrupos que no se superpongan y se denotarán por h; esto se llama el cofactor. El número de puntos en cada subgrupo se denota por r. Asi que:
n=h*r
No vamos a profundizar en el orden y el cofactor en este informe; para nuestro propósito es suficiente con señalar que existen.
¿Cómo se utiliza para el cifrado?
Así, en una curva elíptica tenemos lo siguiente:
- La curva elíptica sobre un campo finito de forma – y2≡ x3 + ax + b (mod p)
- El punto generador o punto base – denotado por G.
- Un valor entero K que, cuando se multiplica con G, da como resultado otro punto P en la curva – P = K*G.
Ahora bien, es rápido y fácil calcular P como se muestra, multiplicando K y G. Pero si queremos calcular K dividiendo P entre G, es decir, K =P/G, entonces es muy difícil o inviable para valores grandes de K.
Esta asimetría, en la que multiplicar es fácil pero dividir (factorizar) es difícil, es la base de la criptografía de curva elíptica y se conoce como el problema logarítmico discreto de curva elíptica (ECDLP). Muchos algoritmos ECC se basan en este problema utilizando curvas elípticas cuidadosamente elegidas, campos para los que no existe ningún algoritmo eficiente.
En el cifrado ECC, K es la clave privada, P es la clave pública y G es el punto generador. Entendiendo el ECDLP como se muestra arriba, sabemos que dado un punto generador G, es muy fácil averiguar la clave pública P en la curva elíptica multiplicando G por la clave privada K. Pero incluso conociendo el punto generador G y la clave pública P, ¡sigue siendo muy difícil calcular la clave privada K!
Ahorro de espacio con los puntos EC comprimidos… a un precio
Ahora sabemos que una clave pública es simplemente un punto en la curva elíptica. Como tal, tendrá una coordenada X y una coordenada Y. Como recordatorio, la ecuación de la propia curva elíptica es
y2 ≡ x3 + ax + b (mod p)
Por tanto, si conocemos x, podemos averiguar fácilmente dos valores de “y” resolviendo las dos ecuaciones siguientes:
p es un número primo impar, por lo que un valor de “y” sería par y otro impar, y cualquiera de ellos satisfará la ecuación.
Así que no necesitamos usar coordenadas {x,y} en la clave pública; podemos simplemente usar {x, [par] o [impar]} para nuestras coordenadas x, con par o impar denotado por un bit de paridad extra llamado Punto EC Comprimido. Haciendo esto podemos ahorrar algo de espacio, lo cual es útil para cifrado en red ya que son menos datos a transferir.
Sin embargo, es en este punto donde encontramos la vulnerabilidad en la implementación de OpenSSL del algoritmo Tonelli-Shanks, que se utiliza para calcular los dos valores de la raíz cuadrada que nos dan y1 e y2. Básicamente, gracias a una implementación poco cuidadosa, el problema en OpenSSL puede desencadenarse al hallar el valor de y a partir de x si la clave pública utiliza coordenadas en el formato de punto EC comprimido.
¿Cómo se utiliza en los certificados SSL?
Teniendo todo esto en cuenta, podemos ver una serie de cosas cuando observamos un certificado SSL que utiliza criptografía de curva elíptica, como se muestra en la Figura 2:
Como vemos, en los certificados SSL tenemos los siguientes campos
- Clave pública (pub) = es P, un punto de la curva; es decir, coordenadas x e y. Puede estar en formato comprimido.
- Prime = es el número primo p, que se utilizará como (mod p)
- A y B = estos dos definen la curva, es decir, y2 ≡ x3 + ax + b (mod p)
- Generador = Es el punto base de la curva por el que se puede calcular cualquier otro punto de la misma.
- Orden y Cofactor = Denotan el orden y el cofactor de la curva. (De nuevo, no los utilizaremos para este informe).
Este certificado puede ser utilizado por el servidor o por los clientes. Una vez que este certificado llega al receptor, éste utilizará la clave pública para cifrar. Si la clave pública está en formato comprimido, el receptor necesita descomprimirla para averiguar y, y para ello necesita resolver la ecuación de la curva – y2 ≡ x3 + ax + b (mod p).
Como la resolución de la ecuación de la curva requiere el cálculo de una raíz cuadrada modular de un número potencialmente grande, se llamará a la función BN_mod_sqrt(). Esta es la función específica en la que la vulnerabilidad CVE-2022-0778 puede ser activada por un certificado especialmente diseñado con valores maliciosos.
Cálculo de la raíz cuadrada modular
Como se ha mencionado, OpenSSL utiliza la función BN_mod_sqrt() para calcular las raíces cuadradas modulares. Según la documentación de OpenSSL, BN_mod_sqrt() devuelve la raíz cuadrada modular de a tal que in2 = a (mod p). El módulo p debe ser un primo o se devolverá un error o un “resultado” incorrecto. El resultado se almacena en in, que puede ser NULL. En ese caso, el resultado se asignará de nuevo. Podemos ver, por tanto, que p debe ser un número primo o el resultado sería incorrecto.
Como se ha mencionado, la vulnerabilidad CVE-2022-0778 reside en la implementación de OpenSSL del algoritmo Tonelli-Shanks utilizado para realizar ese cálculo. Este algoritmo encuentra una raíz cuadrada de un número n módulo p y espera dos parámetros, p y n. Aquí p es un número primo, y n es el número para el que queremos encontrar una raíz cuadrada.
Hay algunas suposiciones y pasos fundamentales para este algoritmo, que se resumen a continuación. (Para obtener información detallada sobre los algoritmos y las pruebas que lo sustentan, consulte la sección de referencias al final de este blog).
- Si se da un número distinto de cero n y un primo impar p, según el criterio de Euler, n tendrá una raíz cuadrada si y sólo si se cumple lo siguiente
![]()
n será un residuo cuadrático.
- Si un número z no tiene raíz cuadrada, entonces según el criterio de Euler se cumplirá lo siguiente
![]()
La mitad de los números enteros entre 1 y p-1 tendrán esta propiedad. z no tendrá raíz cuadrada.
- Como p es un número primo, podemos escribir p – 1 = 2s * Q (Aquí Q es un número impar.)
Ahora bien, si probamos:
![]()
Entonces:
![]()
Aquí, si decimos que t = nQ, podemos tener las siguientes condiciones:
- Si t=1, entonces R será la raíz cuadrada de n, ya que la ecuación se convertirá en
R2 ≡ nt (mod p)
Además, para M=S se cumplirá lo siguiente
t es 2M-1 raíz de 1
- Si t = 0, entonces R será 0 según la ecuación anterior.
- Si t no es 0 ni 1, hay que calcular otro valor de R y t para M-1, y hay que repetirlo hasta que t sea 1 (es decir, que t sea 20, momento en el que R será la raíz cuadrada de n).
- Para encontrar nuevos valores de R y t, podemos multiplicar por un factor b2 que será 2M-2 – la raíz de -1. Para calcular b, zQ se elevará repetidamente al cuadrado.
Si la primera solución es R, la segunda será p-R.
Replicar el problema y depurar el código
El código de prueba del concepto ha sido publicado en GitHub por drago-96 (Riccardo Zanotto). Podemos generar un certificado con parámetros manipulados y utilizar el siguiente comando para replicar el problema con una versión vulnerable de OpenSSL:

Podemos ver que la utilización de la CPU es casi del 100%:

Para la depuración utilizaremos la prueba sencilla de concepto de drago96, que llama a la función vulnerable. Al reunirla y ejecutarla, podemos ver que entra en un bucle infinito causando una utilización de la CPU de casi el 100%.

Observando el certificado podemos ver que utiliza dos valores específicos de p y a, que son 697 y 696 respectivamente.
Si miramos la ecuación de la curva elíptica utilizando esos valores, se convierte en
![]()
donde x3 + ax + b = 696
Como sabemos que el valor de p debe ser primo, debemos notar que 697 no es realmente un número primo. (Se puede escribir como 23 * 87 + 1).
Si probamos este programa con cualquier otro número aleatorio, este problema no se repetirá. (La lógica detrás de usar estos valores específicos, y encontrar más valores de p y a, se discute más adelante en este post).
Al ejecutar OpenSSL con esta prueba de concepto y mirar la llamada a bn_mod_sqrt, podemos ver que los parámetros que se le pasan son 696 y 697, como se muestra en la Figura 7.
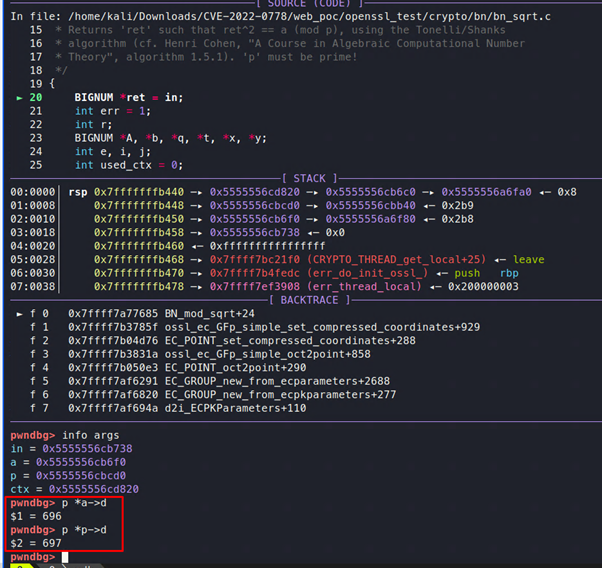
Hay una comprobación para ver si p es impar, o si es 1 o 2, pero no hay ninguna comprobación para ver si p es primo, como se muestra a continuación. Primero se comprueba p:

Luego se comprueba si a es 0 o 1:
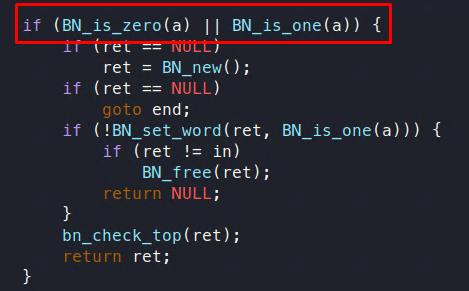
En este punto, la función establece el valor de e como 1 y llama a la función BN_is_bit_set, que básicamente lo convierte en la forma 2e * q como se muestra a continuación, incrementando el valor de e en cada iteración del bucle:
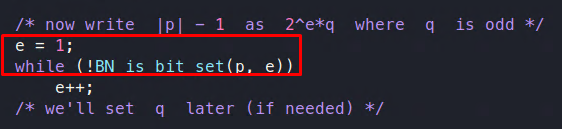
Entonces, e es la potencia de 2, y q es un número impar.
En este punto hay diferentes resultados potenciales dependiendo del valor de e. Si el valor de e es 1 o 2, el código vulnerable no se alcanzará. Pero si el valor de e es 3 o más, entonces se puede alcanzar el código vulnerable, y se utilizará el algoritmo Tonelli-Shanks:
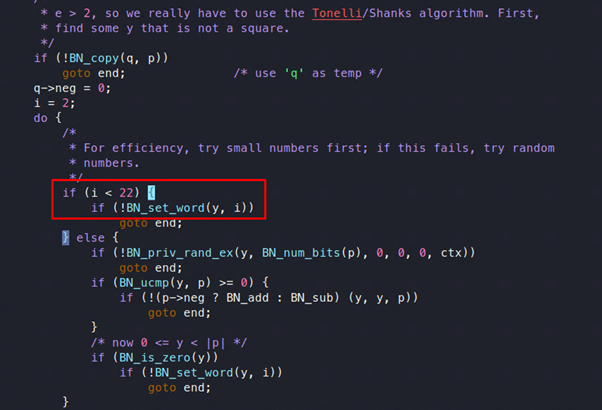
Toma y de 2 a 22 y luego encuentra un símbolo de Kronecker (que es una versión generalizada de un símbolo de Jacobi, que es una versión generalizada de un símbolo de Legendre) con un valor de q.
Esto a su vez se utiliza para encontrar el residuo no cuadrático módulo p. Hay pocas condiciones en este punto:
- Si el valor devuelto es 0 o < -1, entonces el programa cerrará.
- Si el valor devuelto es 1, entonces el bucle do while continuará.
- Si el valor devuelto es -1, entonces el programa pasará al siguiente paso, y habremos encontrado z; es decir, el residuo no cuadrático módulo p.
Entonces calculará el valor de b, y entrará en un bucle while:
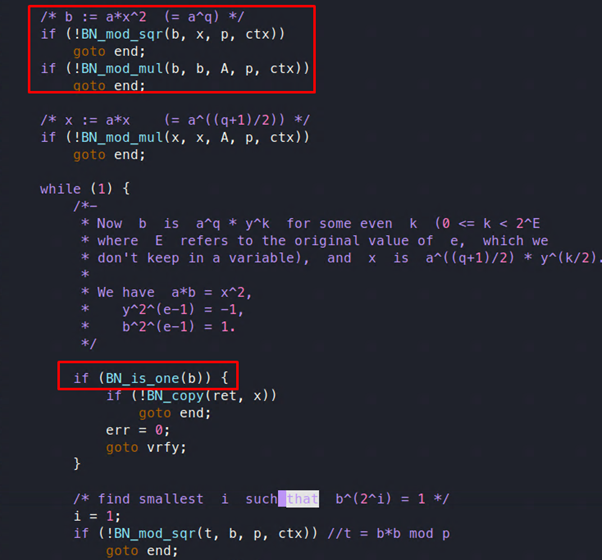
Entonces comprueba si b es uno; si es así, se encuentra la solución. En caso contrario, calculará el valor de t = b2(mod p).
Pero en nuestro ejemplo, t será 1 por primera vez, ya que el valor de p es 697 y b es 696.
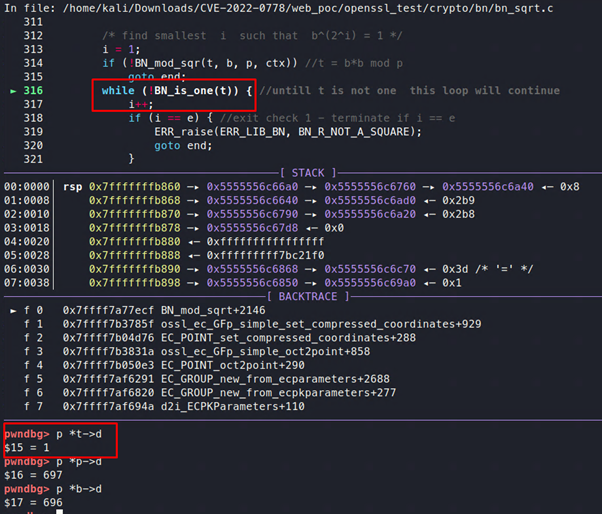
En estas circunstancias, el programa no entrará en el segundo bucle while. Después de realizar algunas operaciones, el valor de t cambiará:
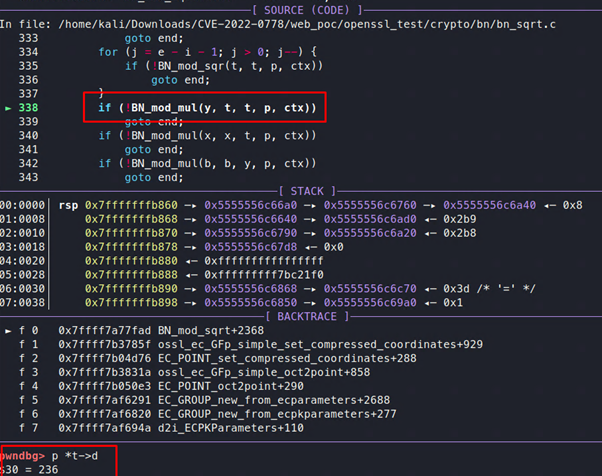
Entonces se moverá el valor de i, que es 1, a e:
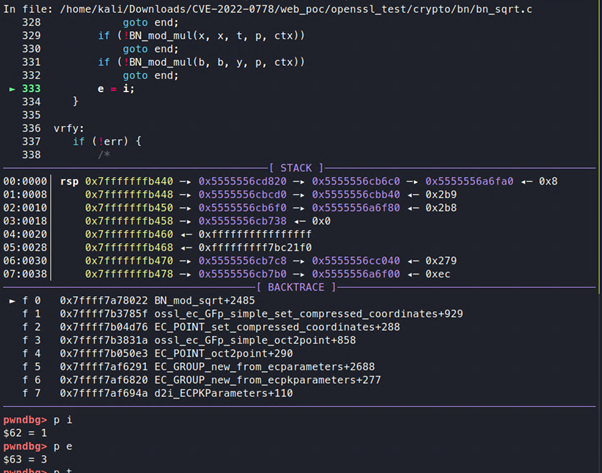
A continuación, irá de nuevo al inicio del bucle while. En este punto t no es 1, por lo que esta vez entrará en el bucle while. El valor de i es 2 pero el valor de e sigue siendo 1, por lo que la condición de salida no se cumple.
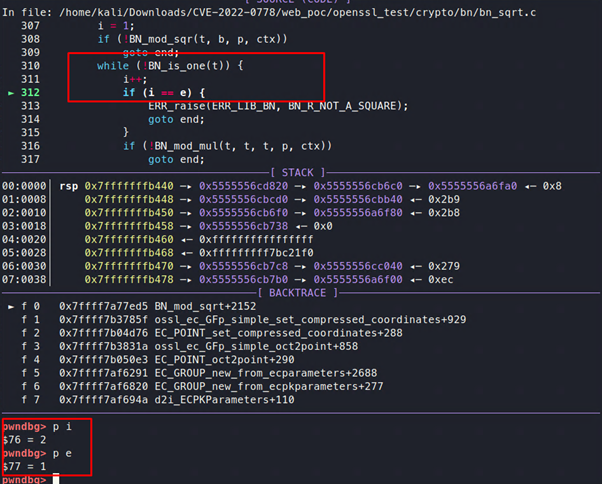
A continuación el proceso llamará a otra función, BN_mod_mul, para calcular el valor de t:
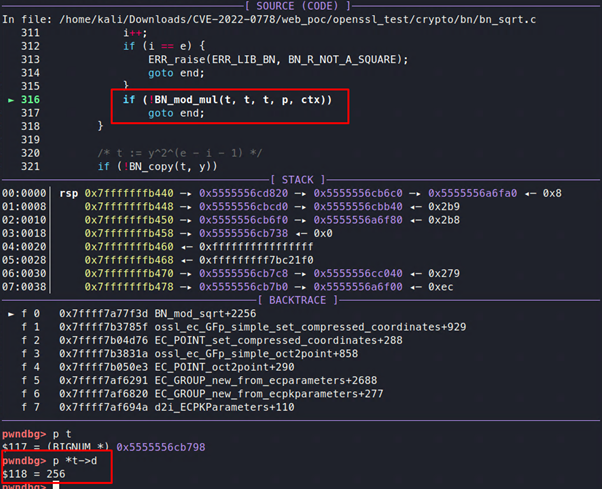
Si recorremos esta función, podemos ver lo siguiente:
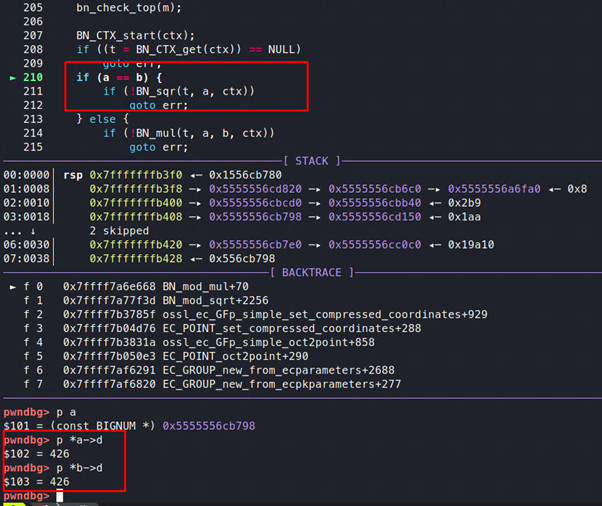
Aquí a y b son iguales, por lo que el proceso llamará a la función BN_sqrt, que calculará t = a2(mod p).
El valor de t nunca será 1, ya que p no es un número primo sino un número compuesto. Por lo tanto, este bucle continuará para siempre. El cálculo interminable e inútil causará así una utilización extrema de recursos y, en última instancia, DoS en la aplicación.
¿Cómo se produce un bucle como este? En este artículo estamos viendo las matemáticas y el código, no las opciones de codificación, pero nuestros colegas de Naked Security tienen un post sobre el CVE-2022-0778 que lleva a una discusión de los bucles extrañamente enmarcados y anidados en el código de OpenSSL que condujo a este problema.
Generando números que pueden causar DoS
Hasta ahora durante la depuración hemos utilizado p=697 y n=696 como valores. Pero hay muchos pares de números que pueden causar este bucle infinito (y por lo tanto el DoS). Podemos establecer fácilmente las condiciones para tales pares:
- p debe ser un número impar compuesto. (De nuevo, si es un número primo, el valor de t se convierte en 1 y salimos del bucle).
- Como se mencionó anteriormente en el blog, si p es un número primo impar, entonces podemos escribir p-1 como
p-1 = 2Q * S
Ahora necesitamos un valor de e >= 3, así que usamos 3. Esta ecuación se convierte en
p-1 = 23 * 2c * S (donde c=Q-3) , que podemos escribir como
p-1 = 8 * 2c * S
Esto significa que p-1 debe ser un múltiplo de 8. Podemos escribirlo como
p-1 = 8 * d * S
Ahora si calculamos p, será
p= 8*d*S+1
Aquí S debe ser un número impar.
- Hemos visto cómo se calculaba el símbolo de Kronecker de 2 a 22 con p:
- Si es 1, continuamos el bucle.
- Si es 0, descartamos ese valor.
- Si es -1, ese es el número.
Basándonos en esto podemos escribir un programa sencillo en C que pueda generar varios pares problemáticos para p y p-1.
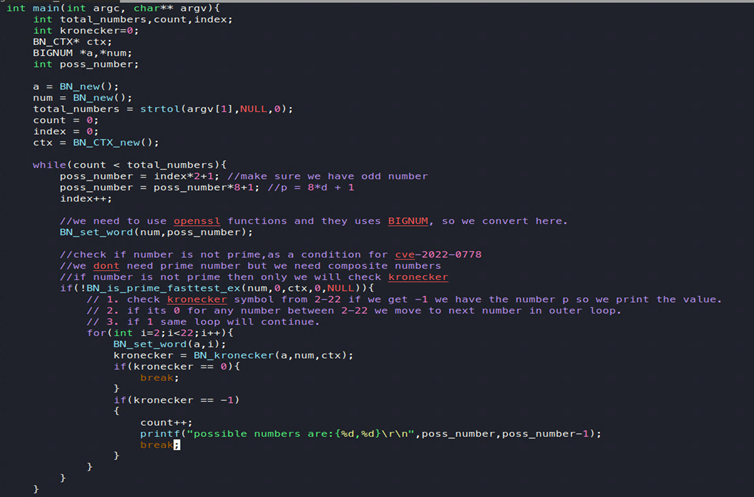
Si ejecutamos este programa, obtenemos lo siguiente
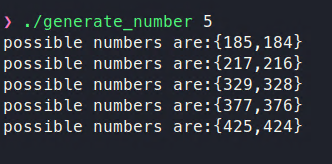
El usuario de Twitter fwarashi ha explicado esto en detalle en un post. (En esa URL también hay un programa de ejemplo en python).
Como vemos en la Figura 20, algunos otros pares de números que pueden causar el DoS CVE-2022-0778 son (184,185), (328,329), (376,377), (424,425) y (472,473). Hay más, pero para ver brevemente dos conjuntos que encontramos:
y2 ≡ 184(mod 185) – es decir, x3 + ax + b = 184
y2 ≡ 328(mod 329) – es decir, x3 + ax + b = 328
Y se pueden seleccionar los valores adecuados de x,a y b que satisfagan esta ecuación.
Cómo solucionar la vulnerabilidad
En la versión sin parchear de OpenSSL, había un bucle “while” que comprobaba el valor de t, y dentro de él había una condición “if” que comprobaba el valor de i ==e, por lo que el programa se saltaba los casos en los que i>e. Si el valor de i > e, y el valor de t no se convierte en 1 en el caso de un número no primo, se produce un bucle infinito, y el DoS resulta de ello.
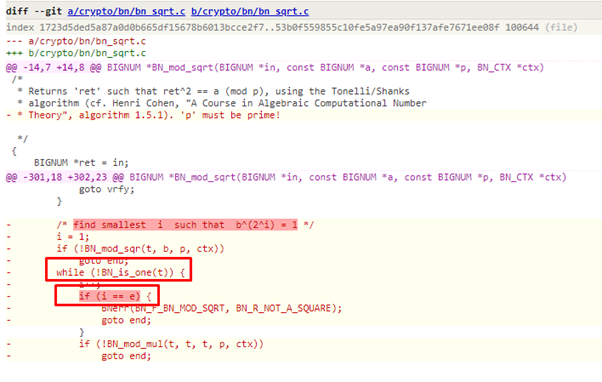
Si observamos el código parcheado, podemos ver que en lugar del bucle “while”, se añade un bucle ”for”. Éste se ejecuta hasta que el valor de i<e, evitando así el problema del bucle infinito.
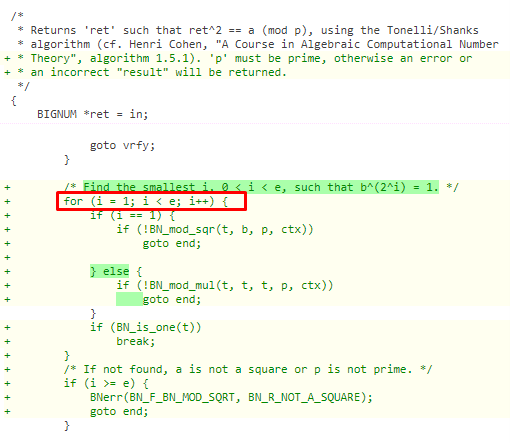
Si el valor de i > e, entonces simplemente se cerrará.
Conclusión
OpenSSL es una librería popular y ampliamente utilizada; no está limitada a ninguna plataforma o aplicación específica. Por lo tanto, la vulnerabilidad CVE-2022-0778 podría afectar a sistemas de todo tipo en todo el mundo. El problema en OpenSSL puede desencadenarse al encontrar el valor de “y” a partir de “x” si la clave pública utiliza coordenadas en el formato de punto CE comprimido, lo que provoca una alta utilización del sistema y puede llevar a un ataque de denegación de servicio.
Dado que la implementación de algoritmos criptográficos es una tarea de nicho, a veces errores como estos pueden pasar desapercibidos. En casos como el de OpenSSL, en el que el código en sí es complejo, la complejidad de las matemáticas en sí puede dificultar la detección de un posible fallo. Sin embargo, no todo está perdido, ya que un análisis cuidadoso puede desentrañar el problema y guiarnos hacia una solución.
Cobertura de Sophos
Los clientes de Sophos IPS están protegidos contra esta amenaza mediante los siguientes sids que comprueban la descarga de certificados maliciosos: 2306976, 2306977.
Referencias y créditos
Esta vulnerabilidad tiene que ver con la criptografía, la teoría de los números, los algoritmos, etc. Durante esta investigación nos ayudaron varios recursos disponibles a través de la web y libros offline. Los siguientes son algunos de los materiales en línea que he utilizado.
Código fuente y prueba de concepto
OpenSSL: https://www.openssl.org/
Repositorio de OpenSSL: https://github.com/openssl/openssl
POC para CVE-2022-0778 de Drago-96 [Riccardo Zanotto]: https://github.com/drago-96/CVE-2022-0778
Análisis de Kurenaif [@fwarashi]: https://zenn.dev/kurenaif/articles/ec2eec4ec7ec52
Para más información
Elliptic Curve Cryptography (de Nakov, Svetlin, Practical Cryptography for Developers [2018]): https://wizardforcel.gitbooks.io/practical-cryptography-for-developers-book/content/asymmetric-key-ciphers/elliptic-curve-cryptography-ecc.html
Hasan, Harady, Curvas elípticas: Un viaje a través de la teoría y sus aplicaciones (2019): https://uu.diva-portal.org/smash/get/diva2:1334316/FULLTEXT01.pdf
Problema de factorización de enteros (HandWiki): https://handwiki.org/wiki/Integer_factorization
“OpenSSL parchea un fallo de DoS de bucle infinito en la verificación de certificados”, Naked Security (blog de Sophos, 18 de marzo de 2022), https://nakedsecurity.sophos.com/2022/03/18/openssl-patches-infinite-loop-dos-bug-in-certificate-verification/)
Algoritmo Tonelli-Shanks (HandWiki): https://handwiki.org/wiki/Tonelli%E2%80%93Shanks_algorithm
Algoritmo Tonelli-Shanks (Wikipedia): https://en.wikipedia.org/wiki/Tonelli%E2%80%93Shanks_algorithm

Dejar un comentario