Transaction security on the internet is where you can find the funkiest vulnerability names.
They include BEAST, Lucky Thirteen, BREACH, POODLE and Heartbleed.
And, of course, FREAK.
FREAK is where you sit yourself on the network between a client and a server, acting as what’s called a Man-in-The-Middle (MiTM).
You don’t literally have to be “in the middle,” of course – you just have to be somewhere on the same network, which could be at another table at the coffee shop, in the car park outside someone’s office, or logged in remotely to a server inside an ISP’s operations centre.
When you see a TLS connection starting up (e.g. to a secure website), the FREAK attack involves trying to trick both ends into accepting what’s called an export-grade cipher instead of a proper one.
Strictly speaking, the ciphers themselves aren’t export-grade, because you still use full-strength algorithms and follow proper protocol.
But EXPORT ciphers use cryptographic keys that are deliberately weakened so that everything looks encrypted, yet a well-heeled adversary like the NSA could crack your traffic if it wanted to.
It’s a bit like buying a top-of-the-range combination safe, but carefully dialling in all the numbers each morning so you can open the safe quickly during the day by just twisting the dial one last time.
According to last century’s US regulators, export-grade ciphers made it safe to sell cryptographic software to potential enemies because their traffic would always be crackable.
The problem with EXPORT
The problem today, of course, is that the EXPORT key lengths were chosen to be just about crackable in the 1990s, but never extended to keep up with advances in processor speed.
That’s because export ciphers were abandoned by the US in about 2000.
They were a silly idea from the start: US companies just imported cryptographic software that had no export restrictions, and hurt their own software industry.
Of course, once the law-makers gave way, the EXPORT ciphersuites become superfluous, so everyone stopped using them.
Sadly, a lot of cryptographic toolkits, including OpenSSL and Microsoft’s SChannel, kept the code to support them, so you (or, more worryingly, well-informed crooks) weren’t stopped from using them.
And, in 2015, the FREAK team found that export-grade RSA, which uses 512-bit keys, was crackable in about two weeks on a decent $2000 laptop, or in just 12 hours (at $100 per key) using Amazon’s cloud.
The solution for server operators was simple: stop supporting EXPORT ciphers.
Here we go again
Well, the FREAK team, or at least some of them, are back with more EXPORT cipher shenanigans.
This time, they’ve attacked a cipher called Diffie-Hellman-Merkle (DHM), often, and with a rather casual disrespect for Ralph Merkle, abbreviated to Diffie-Hellman (DH).
The attack is called LOGJAM. (We’ll explain the pun shortly.)
DHM is a way – in fact, the first published and practicable way – of agreeing on an encryption key without having to exchange it in advance using a separate, secure channel such as a courier service.
As you can imagine, internet commerce would be useless if you had to visit the head office of every online store first to get a secret password printed out before you could buy anything.
DHM provides an algorithm for two parties to use an untrusted, unencrypted communications medium such as the internet to share a secret unsniffably.
Just like the RSA algorithm, DHM was subject to EXPORT cipher regulations until 2000, and, like RSA, the equivalent of its key size was limited to 512 bits.
So, the LOGJAM researchers decided to measure just how weak 512-bit DHM has become today, and they found something interesting.
Exponents and logarithms
We’re not going to explain exactly how it all works here; we’ll just note that DHM relies on a special sort of exponentiation (repeated multiplication, like 2×2×2 = 23 = 8) that is easy to compute, but as good as impossible to reverse.
If you remember your school mathematics, an exponent done in reverse is a logarithm, or log for short.
2 to the exponent 3 is 8, so log to the base 2 of 8 is 3.
Numerically, 23 = 8, so log28 = 3.
Calculating the third power of 2 in your head is easy, but working out log28 is much trickier.
In fact, it’s easiest to start the other way around and use approximation: keep on multiplying 2 by itself until you hit, or get close to, the answer you’re looking for.
DHM uses a special sort of calculation called modular exponentiation, which is even harder to reverse to find a logarithm.
The trick is not to do straight exponentiation, but to take the remainder, or modulus, after dividing each result along the way by a specially-chosen prime number, like this:
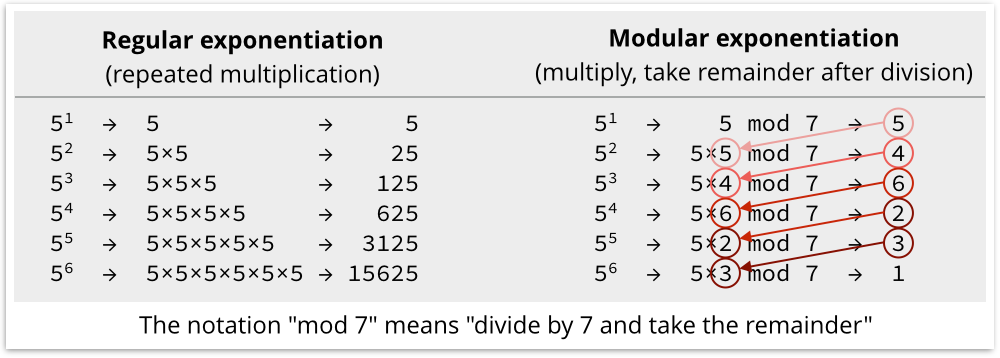
In DHM, solving gx mod p = V for x is as good as impossible, assuming that the numbers involved are big enough to stop you doing it by trial and error.
In the above equation, where all the values involved are positive whole numbers, x is known as a discrete logarithm, and the impracticability of solving for x is known as the discrete logarithm problem.
Cracking DHM
However, as the LOGJAM researchers found, DHM with a 512-bit value of p is just about crackable by an individual with patience, or by a crook with a botnet of a few thousand computers.
They used a two-stage process to do it.
First, they used a technique called the Number Field Sieve on a chosen prime p, plus some heavyweight linear algebra, to pre-calculate a special data set.
The work wasn’t trivial: it took about a week and needed about 3000 CPU cores.
Thereafter, using their pre-calculated data, they could solve gx mod p = V, albeit only for their pre-selected value of p, in about 90 seconds.
JAMming the LOGs
Clearly, 512-bit DHM primes are not strong enough, but we already knew that because they’re EXPORT quality, and EXPORT ciphers were made to be cracked.
But what LOGJAM does is take the second part of the log-solving – the ability to find within 90 seconds any discrete logarithm – and parlay it into an real-time attack.
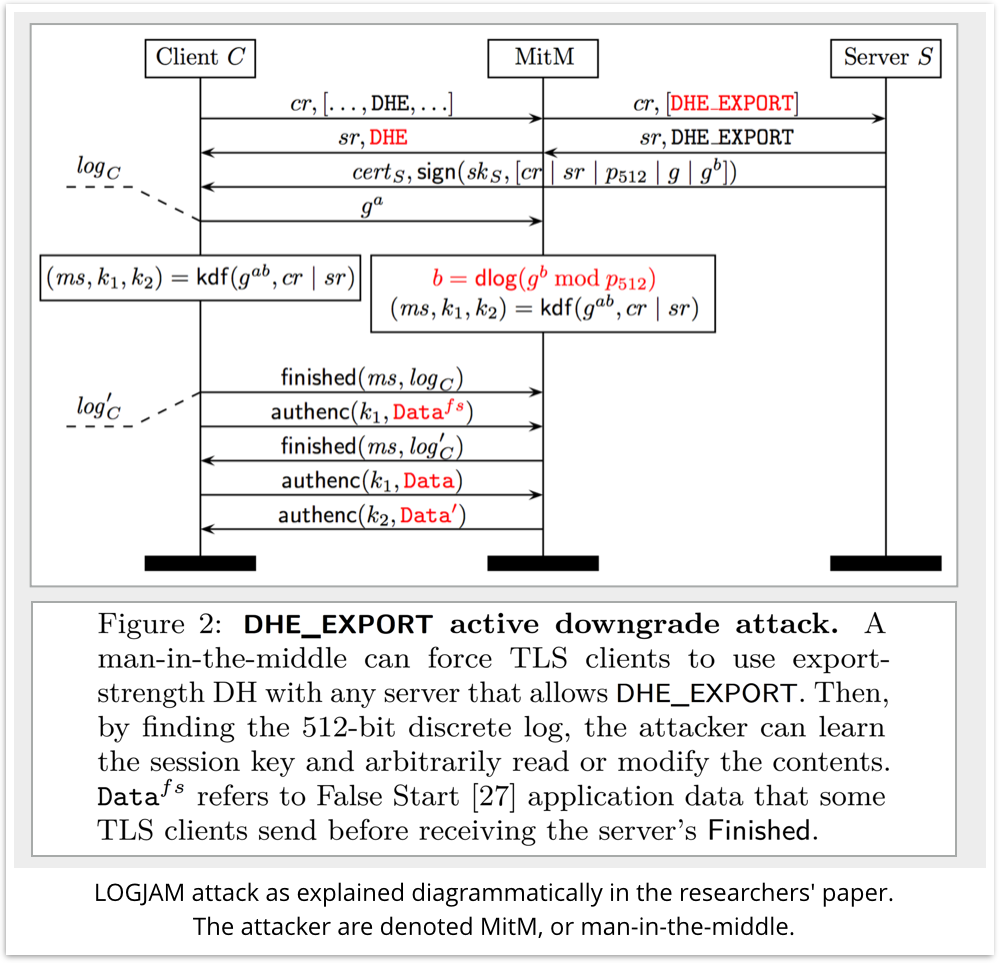
We shan’t go into the details, but the diagram given in the paper itself should help you if you have some mathematics and a bit of cryptography:
Due to a weakness in the TLS protocol itself, the LOGJAM crew figured out how to intercept a client request for a non-EXPORT DHM cipher, pass it onto the server as an EXPORT-quality request, and to forge the reply to the client so it didn’t notice the deception.
The attackers essentially act as an “encryption strength shifter” between client and server.
They can simulate the server cryptographically because they know how to crack the discrete LOG problem for 512-bit primes, whereupon they JAM the forged results into their own replies.
Because the connection between the MiTM and the server is only export-grade, the attackers can extract the session keys agreed during the TLS setup, and therefore read and modify the rest of the session’s traffic.
That’s bad.
What to do?
Easy! Don’t let your server accept EXPORT cipher requests.
That means 512-bit DHM ciphers will be never be allowed, so the LOGJAM attack will be blocked at step one in the diagram above. (The request tagged DHE_EXPORT will fail right at the outset, which means “game over” for the attacker.)
There’s more
After all that, the LOGJAM paper is about much more than just the vulnerability.
It’s about the long-term safety of DHM.
The researchers wanted to know whether they could crack bigger DHM keys in the same way – putting in a sufficiently massive pre-calculation effort to reduce the logarithm-finding time so it could be done “live”.
If so, they wouldn’t need LOGJAM to force a downgrade to 512-bit DHM primes, because they could attack non-EXPORT ciphers, too.
Fortunately, they couldn’t do it: the pre-calculations needed for 768-bit DHM primes were beyond their computational powers.
But they produced evidence to suggest the following:
- An academic establishment with sufficient time and resources (e.g. passionate cryptographers, supercomputers, big server farms, dedicated crypto-cracking hardware) could probably handle 768-bit DHM primes.
- The NSA, and analogous national bodies in other countries, could maybe, just maybe, handle 1024-bit DHM primes.
(They didn’t use those words, of course. That’s our paraphrasing, but we think it’s close enough.)
Remember, however, that each mega-pre-calculation effort would only solve DHM for a single prime number p, which ought to mitigate the risk from “maybe” to “highly unlikely.”
Sadly, because DHM primes aren’t supposed to be crackable, and don’t have to be unique, many servers use standard primes that are hard-wired into the cryptographic libraries they use, or pick their own p but use it indefinitely, storing it across reboots and even between software updates.
Indeed, the researchers found that close to 18% of the websites in the Alexa “Top One Million” list use the same 1024-bit DHM prime for their Diffie-Hellman-Merkle cipher operations.
A further nine primes would catch another 7%, meaning that about a quarter of the Top 1,000,000 sites share just 10 different DHM primes.
That’s bad.
What to do?
Two good ideas are: use longer DHM primes, and change your primes regularly.
So:
- Get rid of all EXPORT-grade ciphers. They were already a bad idea last century when they were still required by US law.
- Consider reconfiguring your servers to use 2048-bit DHM primes. That way, you neatly sidestep the argument about whether 1024-bit primes are actually crackable or not.
- Consider regenerating your servers’ DHM primes on a regular basis. Even if the NSA can crack them, it has to crack them one at a time, so every time you regenerate yours, the NSA’s previous effort is wasted.
For the record, finding five 2048-bit DHM primes on my three-year-old laptop took, successively: 14″, 2’07”, 43″, 1’25” and 55″.
Clearly, therefore, it’s not something you’d do for every connection, but recomputing DHM primes once a week (long enough to thwart even the LOGJAM attack described in the paper) is not computationally onerous.
Every time you take the lead, the crooks, ipso facto, fall behind.
Note. Server products from Sophos (Secure Email Gateway, Secure Web Gateway, UTM & Next-Gen Firewall and Mobile Control) don’t accept EXPORT ciphers, so they can’t be Logjammed.
