The big, bad bug of the week is called Zerologon.
As you can probably tell from the name, it involves Windows – everyone else talks about logging in, but on Windows you’ve always very definitely logged on – and it is an authentication bypass, because it lets you get away with using a zero-length password.
You’ll also see it referred to as CVE-2020-1472, and the good news is that it was patched in Microsoft’s August 2020 update.
In other words, if you practise proper patching, you don’t need to panic. (Yes, that’s an undisguised hint: if you haven’t patched your Windows servers yet from back in August 2020, please go and do so now, for everyone’s sake, not just your own.)
Nevertheless, Zerologon is a fascinating story that reminds us all of two very important lessons, namely that:
- Cryptography is hard to get right.
- Cryptographic blunders can take years to spot.
The gory details of the bug weren’t disclosed by Microsoft back in August 2020, but researchers at Dutch cybersecurity company Secura dug into the affected Windows component, Netlogon, and figured out a bunch of serious cryptographic holes in the unpatched version, and how to exploit them.
In this article, we aren’t going to construct an attack or show you how to create network packets to exploit the flaw, but we are going to look at the cryptographic problems that lay unnoticed in the Microsoft Netlogon Remote Protocol for many years.
After all, those who cannot remember history are condemned to repeat it.
Authenticating via Netlogon
Netlogon is a network protocol that, in its own words, “is a remote procedure call (RPC) interface that is used for user and machine authentication on domain-based networks.”
At 280 pages, the Netlogon Remote Protocol Specification – it’s an open specification these days, not proprietary to Microsoft – is a lot shorter than Bluetooth, but far longer than any programming team can take in over a period of months or years, let alone days or weeks.
Its length comes in part from the fact that there are often many different ways of doing the same thing, somtimes with multiple different fallback algorithms that have been kept on to ensure backwards compatibility with older devices.
Ironically, perhaps, Section 5, Security Considerations, has just two short parts: a one-page subsection entitled Security Considerations for Implementors, and a brief (though admittedly useful) table called Index of Security Parameters that links to various important sections in the specification.
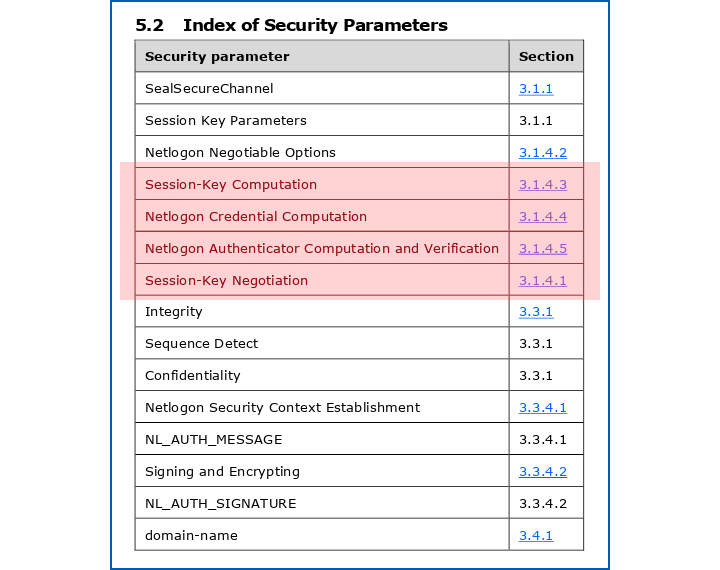
The highlighted items are the ones we look at in this article.
Getting started with Netlogon
A client computer that wants to communicate with a Netlogon server such as a Windows domain controller starts by sending eight random bytes (what’s often called a nonce, short for number used once) to the server.
The server replies with 8 random bytes of its own, as explained in section 3.1.4.1, Session-Key Negotiation:
REQUEST --> ClientChallenge (8 random bytes, e.g. 452fdbfd2e38b9e0) -->
REPLY <-- ServerChallenge (8 random bytes, e.g. 7696398fe5417372) <--
As shown above, Microsoft refers to these nonces as ClientChallenge (CC) and ServerChallenge (SC) respectively, if you want to match up this discussion with the protocol documentation.
Both sides then scramble up the two random strings together with a shared secret to concoct a one-off encryption key, known as the SessionKey (SK).
On a Windows network, the secret component is the domain password of the computer you’re connecting from.
On the client, this is stored securely by Windows in the registry; on the domain controller, it’s stored in the Active Directory database.
This SessionKey scrambling is done using the keyed cryptographic hash called HMAC-SHA256.
The algorithm is specified in section 3.1.4.3.1, AES Session-Key, and in pseudocode it looks like this:

Assuming that the client requesting access has the same password stored locally as the Netlogon server has on record centrally, and given that each side has already told the other its 8-byte random challenge, both sides should now have arrived at the same, one-off SessionKey value (SK) to secure the rest of their communication.
This session key setup avoids using the secret password directly in encrypting Netlogon traffic, and ensures a unique key for each session, into which both parties inject their own randomness. (This is a common approach: setting up a WPA-2 wireless connection using a pre-shared key follows a similar process.)
In theory, the server could blindly assume that the client knows the real password by simply accepting encrypted function calls immediately; if the client had cheated so far by using a made-up password, the requests wouldn’t decrypt properly and the ruse would fail.
Good practice, however, says that each end should verify the other first, for example by encrypting a known test string that the other end can validate, and that’s what happens next.
Obviously, the client can’t share the session key directly because that would let anyone else on the network sniff it out and hijack the session.
Instead, the client proves that it knows the session key by encrypting the ClientChallenge that it committed to at the start, using the SessionKey it just calculated.
Microsoft calls this the Netlogon Credential Computation, detailed in section 3.1.4.4.1:

At the other end, the server does the same thing in reverse, and verifies that the original ClientChallenge comes out correctly when the ciphertext is decrypted with the session key.
At this point, it looks as though an imposter client is stuck.
Without the right secret password, which you can only get by already having administrator-level access to a trusted computer on the network, you won’t get the same session key as the server.
Without the right session key, you won’t produce an encrypted version of your original 8-byte random string that the server will accept to authenticate you.
A chink in the armour
At this point, if you’re interested in cryptography, you’re probably wondering, “What on earth is the encryption algorithm dubbed AES-128-CFB8 in the pseudocode above?”
Let’s investigate.
AES, short for Advanced Encryption Standard, sounds like a good choice because it’s currently accepted as a strong algorithm with no known security holes.
Also, a key size of 128 bits is currently regarded as satisfactory because it would take too long to try all possible 2128 keys, even if you harnessed all of the world’s computing power for yourself.
For the record: AES doesn’t use any internal calculations that could be sped up with so-called quantum algorithms, so it is considered post-quantum secure. Even if a truly powerful quantum computer were built tomorrow, it wouldn’t be of any special use, so far as we know, in cracking AES faster than we can with regular computers today.
But algorithms like AES can be used in many different modes, and not all of them are suitable for all purposes.
The best-known mode, which you can think of as “straight encryption”, is called AES-128-ECB, and it scrambles 16 bytes of input at a time, directly producing 16 bytes of output.
Note that we’ve simplified these diagrams by pretending that AES-128 works on 4 bytes (32 bits) at a time instead of 16 bytes (128 bits), but the underlying principles are still clear:
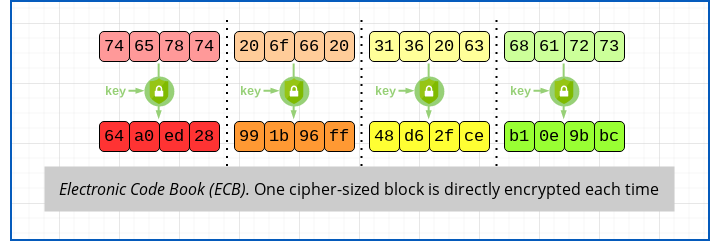
ECB stands for Electronic Code Book, because the cipher in this mode does indeed work like an unimaginably large codebook.
The codebook moniker is entirely theoretical. In practice, you would need a different codebook for every one of the 2128 different keys, with each book listing every one of the encryption values for each of the 2128 different 16-byte input strings. And you would need a further 2128 (that’s 300 million million million million million million) codebooks to list all the possible decryptions, too, if you ever had the space or time to unscramble what you had previously encrypted.
Unfortunately, the simplicity of codebook mode is also a weakness, because any time there is repeated text in one of the input blocks, you’ll know because you’ll get a repeat in the ciphertext, too:
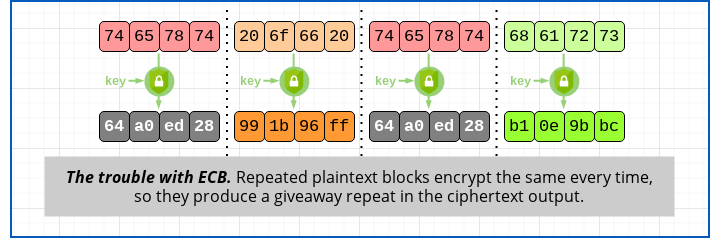
At best, ECB leaks whether there are any patterns in the input, something that an encryption algorithm should conceal.
At worst, it means that if ever you figure out what the plaintext was in one part of the input – a chapter heading, for example, or part of a Bitcoin address – you will automatically be able to decrypt that text everywhere else it appears.
Various solutions exist to use block-based encryption algorithms so they don’t reveal repeated patterns, and one of them is Cipher Feedback (CFB) mode, which works like this:
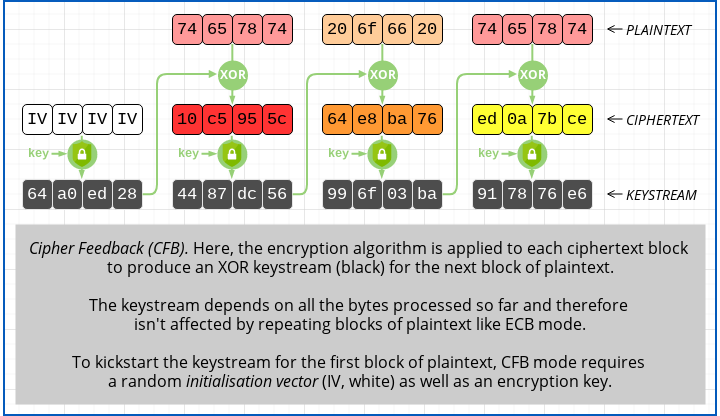
Instead of encrypting the plaintext blocks with AES each time, you encrypt the last block of ciphertext instead, and then XOR that “keystream” with the next block of plaintext.
That way, even if you get two identical plaintext blocks in a row, the ciphertext won’t repeat.
Of course, there is no ciphertext block to use at the outset, so AES-128-CFB mode requires not only a key of 16 bytes for the encryption engine, but also an initialisation vector (IV) of 16 bytes as an up-front input to get the keystream started.
Note that the IV can, and usually is, shared along with the ciphertext – the IV doesn’t need to be kept secret, because the secrecy of the encryption is provided by the key that controls the AES encryption engine.
Nevertheless, a CFB initialisation vector should be chosen randomly, and should never be re-used, especially with the same AES key.
CFB8 explained
One disadvantage that AES-ECB and AES-CFB have in common is that until you have a full 16-byte block of input, you can’t produce any output, because they can’t work on partial blocks – AES is designed to mix-and-swap-and-mince-and-munge chunks of 128 bits at a time.
That also means you are stuck if you have any leftover bytes at the end, for example if you have 67 bytes to encrypt, which is 4×16 + 3.
You need to figure out a way to pad out the last block to the right size, and then reliably work out whether there were any extra bytes added on that need to be stripped off when you decrypt the data.
One solution to this is AES-CFB8, a mode that we have never heard of anyone using in real life before, but that is designed to use a full 128-bit AES mixing cycle for every byte of input, so you can encrypt even just a single character without any padding.
Instead of encrypting the last full block of ciphertext to create the next full block of keystream data, you use just the first byte of the keystream each time and XOR it with one plaintext byte rather than a 16-byte plaintext block.
Then you chop off the keystream byte you just used and add the new ciphertext byte on at the end of the keystream, giving you a full block of data to encrypt to generate the next keystream byte:
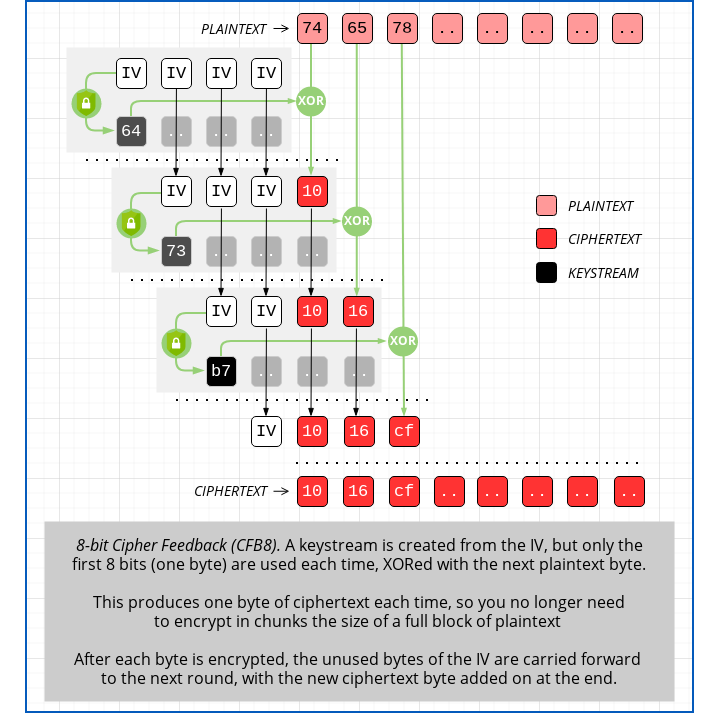
Netlogon CFB8 considered harmful
Sadly, the way that Netlogon uses AES-128-CFB8 is significantly less secure than it should be.
Secura researchers spotted the problem very quickly when perusing the Microsoft documentation, where the algorithm is not defined generically (as we listed it above), but given in a dangerously simplified form.
Section 3.1.4.4.1 specifies the AES Credential [Computation] process as follows:
If AES support is negotiated between the client and the server,
the Netlogon
credentials are computed using the AES-128 encryption
algorithm in 8-bit CFB
mode with a zero initialization vector.
[Sk below is short for SessionKey]
ComputeNetlogonCredential(Input, Sk, Output)
SET IV = 0
CALL AesEncrypt(Input, Sk, IV, Output)
You probably spotted the cryptographic blunder already: “the credentials are computed […] with a zero initialization vector.”
As we already mentioned, IVs are supposed to be randomly chosen, and used only once with any key – indeed, that’s why they are often referred to as nonces, for numbers used once.
But there’s an even bigger problem with an all-zero IV in CFB8 mode, as Secura discovered.
You can visualise the problem if you use an all-zero IV plus an all-zero block of plaintext bytes:
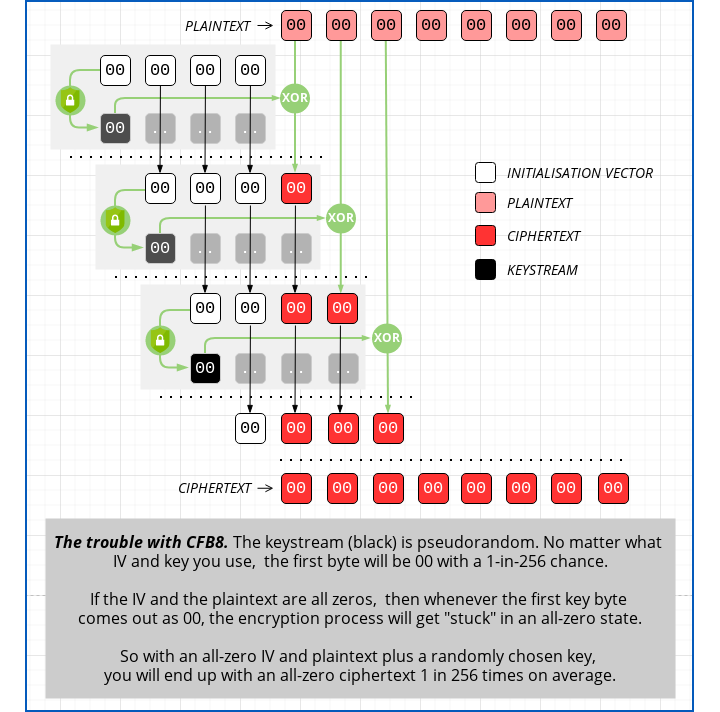
Because AES is a high-quality cipher with no known statistical biases, you can put in any input and encrypt it with any key, and the chance of each individual bit in the output being zero (or one) is 50%.
Every output bit’s value is like a digital coin toss.
So the chance of the first output byte being zero is the same as the chance that the first 8 output bits are all zero, which is 50% × 50% × 50% … eight times over (50% is just another way of writing 0.50, which is the same as 1/2).
50%8 is 2-8, or 1/256.
Remember that probability.
In the diagram above we’ve assumed that the first output byte did indeed come out as zero, and you can see that if that happens, the entire encryption process essentially gets “locked into” an all-zero state.
The keystream byte (black) comes out as 00, so when you XOR it with the first plaintext byte (pink) of 00 you get a ciphertext byte (red) of 00.
Then, when you chop the first 00 off the left hand end of the IV (white) and append the new ciphertext 00 at the end, you are right back where you started, with another all-zero IV and a remaining plaintext buffer of all zeros.
When you encrypt the “new” IV with the key, you get exactly the same result as before, because all your inputs are the same again, and out comes another keystream byte of 00, which XORs with the next plaintext 00 to produce another ciphertext byte of 00, which feeds back into the IV to make it all zero again.
How to trick Netlogon
Secura’s researchers quickly realised what would happen if they tried to authenticate to a Netlogon server over and over again using a ClientChallenge nonce consisting of 8 zeros.
Roughly once in every 256 times the server would randomly concoct a session key for which the correctly-encrypted version of their all-zero ClientChallenge…
…would itself be all zeros.

One in 256 times the key chosen gave all-zero output too.
In other words, by submitting a ClientChallenge of 0000000000000000 and then blindly also submitting a Netlogon Credential Computation (see above) of 0000000000000000, they’d get the credential computation correct by chance 1/256 of the time, even though they had no idea what the right SessionKey value should be because they had no idea what secret password to use.
Simply put, 1/256 of the time, they ended up in a situation where they could always produce correctly-encrypted data to transmit to the server, without having a clue what the password or session key was, as long as they only ever needed to encrypt zeros!
Better yet, the server would automatically notify them when they hit the jackpot by accepting their credential submission.
Surely that’s not exploitable?
By now you are probably thinking, “What’s the chance that every time they needed to submit an encrypted authentication token or to supply encrypted password data, they’d only ever need to encrypt zeros?”
We wondered that too, but our intrepid researchers found a way.
One of the Netlogon password functions, NetrServerPasswordSet2 (section 3.4.5.2.5), can be called remotely from a Netlogon session that has already got past the Netlogon Credential Computation check.
This function, which does what its name suggests and changes the server password, requires the caller to correctly encrypt two chunks of data:
- The original
ClientChallenge, treated as a 64-bit number, with the current time (in what’s known as “Posix seconds” or Unix epoch form) added to it. This data is used as an authentication check to ensure it’s still the same client program trying to do the password change. - A buffer of 516 bytes that specifies the new password, formatted as (512-N) bytes of random data, followed by N bytes specifying the password, followed by the password length N expressed as a 4-byte number.
The ClientChallenge is all zeros, because that was needed to get the exploit started in the first place, but the current time in Posix seconds is something close to this:
$ date --utc +%s 1600300026
Posix time denotes the number of seconds since the start of the Unix epoch, which began, by definition, at 1970-01-01T00:00:00Z, a date now more than 50 years in the past.
The researchers found themselves on the horns of a dilemma: the ClientChallenge was zero, but the time was not, so the sum of those two numbers couldn’t be zero, and therefore wouldn’t encrypt to zero…
…and therefore the attackers would need the original session key after all, and to get the session key they would need to know a valid password for a suitable computer on the network.
What to do?
Well, the researchers just pretended it was 1970 all over again, used a timestamp of zero added to a ClientChallenge of zero…
…and the server didn’t mind – there was apparently no check to see if the timestamp was decades in the past.
Of course, the 516 all-zero bytes that the researchers now needed to supply in the encrypted password buffer forced them to specify a password length of zero, which you might think would be disallowed by the server.
But the researchers tried it anyway…
…and the server didn’t mind that either, setting its own Active Directory password to <no password at all>.
What next?
Happily – or perhaps slightly less unhappily – the password change that they were able make didn’t reset the server’s actual login password, so the researchers couldn’t simply login directly and take over the server via a conventional Windows desktop.
However, they did report that by changing the Active Directory password of the domain controller itself, they were able to:
extract all user hashes from the domain through the Domain Replication Service (DRS) protocol. This includes domain administrator hashes (including the ‘krbtgt’ key, which can used to create golden tickets) that could then be used to login to the Domain Controller (using a standard pass-the-hash attack) and update the computer password stored in the Domain Controllers’s local registry.
In other words, complete network compromise.
All because of an over-simplified cryptographic specification that involved the cardinal sin of an all-zero initialisation vector every time.
Of course, that flaw was compounded by several other programmatic oversights where stricter attention to security and correctness could have prevented this attack, including:
- Allowing an all-zero
ClientChallengein the first place. We’d assume that the most likely cause of an all-zero buffer at the start of the Netlogon process would be an incorrectly initialised or buggy client program, so we’d reject it as a precaution anyway. - Allowing a zero-length password. Given that Windows already has a secure mechanism for storing shared secrets, and relies on it heavily anyway, it seems unnecessary to allow blank passwords at all, even for accounts where no humans are ever expected to log on.
- Allowing a date-based authentication field in which the timestamp could not possibly be correct. We’d be inclined to treat this as a warning of a buggy client or an attempt to pull off a security trick.
What to do?
This bug opens a serious security hole to anyone already inside your organisation, and perhaps even to outsiders, depending on the topology of your network.
If you haven’t applied the August 2020 patch yet, you need to do so – you aren’t just letting yourself down, you’re letting everyone else down too by making your network an easier target for crooks, and therefore making it more likely that you will be the source of security problems for other people.
In addition:
- Don’t take cryptographic shortcuts such as choosing an encryption mode that’s convenient for your application, but then taking liberties with how you use it because that’s convenient for your programmers.
- Program defensively whenever you are accepting untrusted data, especially if the data can easily be checked for obviously forged or incorrect values such as timestamps 50 years in the past.
- Retire old parts of your products or specifications as soon as you can after better ones are available. Although the exploit in this case relied on updated parts of the Netlogon protocol, such as using AES instead of falling back to older algorithms, you can argue that this bug might have been found far sooner if the protocol specification were not encumbered with so many alternative ways of doing all sort of security-related checks.
But the big thing to remember here is: patch early, patch often.

Malcolm Doody
Typo “Cipher Feeback (CFB) mode” (just above the diagram)
Paul Ducklin
Fixed! Thanks for the, ahem, feedback.
Anonymous
There are still 3 typos in this article.
Paul Ducklin
Well, I just found one. Tell you what. I’ll tell you mine and you can tell me yours, and therefore between us we can do something about all of them.
Mine was a mis-spelling of “documentation”.
What have you got there?
Max
The best explanation of the vuln root cause. Thanks a lot!
Paul Ducklin
Thanks for your kind words. Glad you found it useful!
Pete Corrao
A great read! Thanks for the graphics – they helped a lot with understanding the flow.
Paul Ducklin
A pleasure. Glad you found the graphics useful – they were fun to create but neded up being a LOT of work so I am happy to hear they were worth it!
Jackson Wells
Excellent write up on this exploit. This has helped me greatly.
Paul Ducklin
Thanks for your kind words. Glad you found it useful.
Issam
Hi, I have many questions to ask but first, I’d like to thank you for writing this great article, it has been really helpful.
1. At one point you said: “At the other end, the server does the same thing in reverse, and verifies that the original ClientChallenge […]”.
Did you mean the “ClientCredential” which is sent in input using the NetrServerAuthenticate call? [3.1.4.1] step 5.
2. The researcher Tom Tervoort (in the white paper) said the client is using the NetrServerAuthenticate3 but why not the 1 or 2? [3.4.5.2] & [3.1.4.1] step 5.
3. I didn’t really understand the part with the 50% chance. You said that “[…] the chance of each individual bit in the output being zero (or one) is 50%.”, why?
And how come to the fact that the chance of the first output byte being zero is the same as the chance that the first 8 output bits are all zero?
4. Could you share the code you used to see the anomaly (“try-cfb8.lua”) or explain briefly how you programmed it?
Hoping you could answer my questions, thank you!
Paul Ducklin
1. The client encrypts its original ClientChallenge using its SessionKey, producing the ClientCredential. The server goes in reverse, and decrypts the received ClientCredential using its SessionKey. If an exact copy of the original ClientChallenge emerges from this decryption, then the server assumes that the client knows the correct SessionKey and therefore accepts the ClientCredential as an authentication token from then on.
2. I don’t know. Presumably because NetrServerAuthenticate3 is the currently recommended function to use? The …Authenticate2 and …Authenticate functions are noted as predecessors. If you are going to crack one of them, cracking the latest and greatest version is a better proof of concept that cracking an old version of the protocol. (If you manage to hack Windows XP, no one is going to be terribly impressed. If you do something similar on Windows 10, everyone will be.)
3. Picking a bit randomly is like tossing a coin, so there’s a 50:50 chance of 0 or 1, just like there’s a 50:50 chance of heads or tails. So getting a *byte* (8 bits that are all zero) is like tossing heads 8 times in a row. It will happen on average 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 of the time (one half times one half times one half… etc.), which is 1/256 (2 to the -8).
4. WordPress might mess this up a bit (copy and paste into a decent editor, I guess). I chose 2560 tries because at an anomaly rate of 1/256 you would therefore expect an average of 10 anomalies every run. If the anomalies happened truly randomly you would expect to see one every 2 to the 64/2560 runs, which would take a verrrrrrrry lonnnnnnnnng tiiiiiiiiiiiime.
local cipher = require 'openssl.cipher'
local base = require 'base'
local iv = string.rep('\x00',16) -- Always use an all-zero 16-byte IV
local pt = string.rep('\x00', 8) -- Always use 8 zero bytes as plaintext
local tries = 2560
local weird = 0
for i = 1,tries do
local cfb8 = cipher.new('aes-128-cfb8') -- Use the AES-128-CFB8 cipher
local key = io.open'/dev/urandom':read(16) -- Use a different random key each time
local ct = cfb8:encrypt(key,iv):final(pt) -- Do the 8-byte encryption
-- Print out the key we used and the ciphertext returned.
-- These strings should both be decently pseudorandom.
io.write(string.format('%5d %s %s',i,base.hex(key),base.hex(ct)))
-- The ciphertext and the plaintext should be
-- identical so rarely as for it to be freaky
if ct == pt then
io.write(' ***ANOMALY***')
weird = weird + 1
end
io.write('\n')
end
io.write('\n',weird,' one-in-a-quintillion anomalies in ',tries,' tries.\n\n')
io.write('Rate is 1 in ',math.floor(tries/weird),'\n\n')
Issam
Thank you a lot for taking the time to answer my questions!
Paul Ducklin
No worries, it was worth my time to go back and check the answers :-)