The big “cryptographic cracking” story so far in 2016 is SLOTH, which is not only interesting and important, but also a VUWACONA, making it eye-catching as well.
VUWACONA is short for Vulnerability With A Cool Name, our new acronym for bugs like LOGJAM, FREAK and Poodle.
Like those three previous security problems, SLOTH is the result of modern cryptographic protocols continuing to use superannuated cryptographic algorithms, and needlessly being less trustworthy as a result.
Indeed, the name is both an acronym, short for Security Losses from Obsolete and Truncated Transcript Hashes, and a metaphor.
In the words of the authors of the paper, SLOTH is “a not-so-subtle reference to laziness in the protocol design community with regard to removing legacy cryptographic constructions.”
The SLOTH paper is fairly technical, and relies on quite a lot of cryptographic jargon, making it hard to penetrate if you aren’t a cryptographer already.
Here, we’ll just give a general overview of the problems that were exploited by the SLOTH authors, and what that tells us about our attitudes to cryptography in particular, and security in general.
Why have secure protocols?
Secure internet protocols such as TLS, previously known as SSL, are designed to provide encryption (keep your conversation secret), authentication (know you are talking to the right person) and integrity (be sure that you are reading exactly what the other guy sent).
Secure HTTPS web pages that were protected only by encryption would give you a dreadfully false sense of security when doing online banking: there’s no point in being on a strongly-encrypted internet connection if you’re talking to a crook at the other end.
Authentication over the internet is usually achieved using what are known as digital signatures, based on public-key cryptography, for example using the RSA algorithm.
The other end “locks”, or signs, a message in such a way that when you try to “unlock” it to validate its signature, the unlocking process will fail unless it really was locked by the person you expected.
But using RSA for unlocking and locking is problematic, because the RSA algorithm is very slow, and is usually used only to encrypt very short messages.
Enter the hash
Instead of working on the entire message, which might be a detailed and quite lengthy exchange of cryptographic parameters, cryptographic protocols usually create a cryptographic checksum, or hash, of the message, and sign the hash instead.
Hashing algorithms such as MD5, SHA-1, SHA-256 and SHA-3 produce a fixed-length output that acts as a sort of “digital fingerprint”, so whether your message is one character or 1GB in size, you know in advance how big the hash will be, and can plan, and program, accordingly.
In other words, the authentication process depends on the hash being a reliable placeholder for the message.
If you can fake the hash, you have effectively faked the whole message.
Generally speaking, then, hash functions are judged by how well they mix up their input data to produce the final output, which is usually a lot shorter than the input.
In particular, a hash, denoted here as a mathematical function H(), should have at least these characteristics:
- If you deliberately create two messages M1 and M2 (any two messages; you get to choose both of them) such that H(M1) = H(M2), you have a collision, which undermines the value of H as a digital fingerprint. Therefore you should not be able to construct a collision, other than by trying over and over with different inputs until you hit the jackpot by chance.
- If you know that H(M) = X, but you don’t know my message M, then you should not be able to “go backwards” from X to M, other than by trying different messages over and over until you hit the jackpot by chance.
- If I choose M and tell you what it is, so you can compute H(M) = X for yourself, you should not be able to come up with a different message M’ that also has H(M’) = X, other than by guesswork. (This is much tougher than case 1 because you don’t get to choose any matching pair of hashes from a giant pool of messages. You have to match my hash, not any hash, which squares the effort needed.)
As you can imagine, if a hash function is found to have poor collision resistance (weakness 1 above), then it is prudent to assume that the function is generally flawed, and simply doesn’t mix-and-mince-and-shred-and-liquidise its input well enough to be safe against the other weaknesses, either.
But weaknesses of type 1 are generally much easier to find than the other sorts, and even for a hash function where tricks already exist to produce collisions at will, there may not yet be any practical way of pulling off the other two tricks, which are known in the literature as pre-image resistance.
We are at already that point with MD5.
And we are close to it with SHA-1, at least for attackers with lots of money or computers, so those two algorithms are now banned from many uses, such as signing digital certificates.
She’ll be right…
However, it’s easy to fall into the trap of saying, “Well, if we’re careful, we can still get away with using MD5 and SHA-1, provided that we use them only when an attacker would have to use weakness 3, and provided that we only use it to authenticate short-term data, for example when setting up each connection.”
If you will pardon the analogy, that’s a bit like borrowing a car where the steering has been so badly maintained that it pulls to the left unpredictably, and then driving it anyway.
You could assume that the shoddy steering tells no story at all about how well the rest of vehicle has been cared for; that the brakes are probably OK; and that as long as you keep the speed down, and remember to aim a bit to the right of where you want to go, you’ll be fine…
SLOTH proves a point
The SLOTH authors, and many other cryptographers, begged to differ with those who took the “she’ll be right” approach and were therefore continuing to use MD5 and SHA-1 selectively.
Until now, however, they couldn’t prove that MD5 and SHA-1 were too weak for all uses just because they could be exploited for some sorts of attack.
But all that has changed, because the SLOTH paper shows a number of weak-hash-based attack techniques against TLS that are already either practical, or dangerously close to it.
They also show similar attacks against SSH and IKE that, if not yet practicable, are nevertheless worryingly far from the security that the mathematics claims you should enjoy.
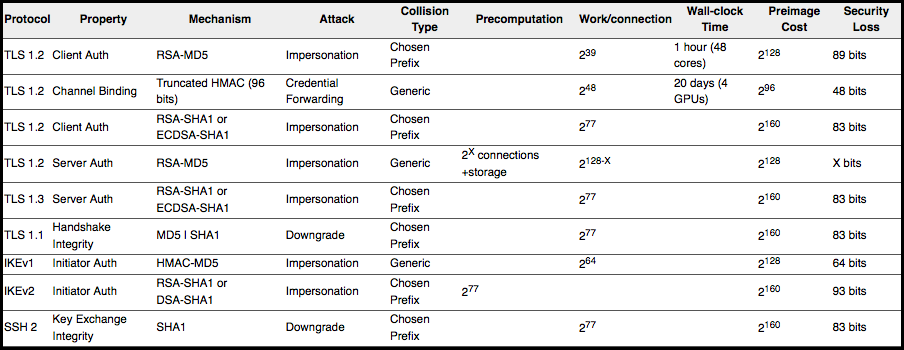
Don’t worry if this table doesn’t make a lot of sense to you, but the deal is that the column labelled “Preimage Cost” gives the number of hash calculations you would need to do in order to guarantee a successful attack by chance, while the “Work/connection” column shows the number of calculations needed to pull off an attack using the SLOTH techniques:
To be sure, cracking SSH sessions by doing 277 calculations in real time per connection is nowhere near practical, at least today, so it’s tempting to say, “So why not keep on using SHA-1 in this context, at least for a bit?”
On the other hand, the “Security loss” column tells you the SLOTH attacks prove that the security you get by allowing SHA-1 in SSH2 key exchanges is a whopping 283 times weaker than it’s supposed to be.
The SLOTH attacks aren’t easy, some of them would be very expensive, and many of them are still currently impossible…
…but, as the saying goes, attacks only ever get faster.
What to do?
Don’t use MD5 and SHA-1. It’s that easy!
Their steering pulls to the left, and that simply isn’t good enough.
Baby sloth courtesy of Shutterstock.

Damon
great article (as always), Paul
Steve
As always!
Paul Ducklin
Thanks, guys! I appreciate your kind words.
Alan Robertson
Wise words Paul but remember you’re relying on the server you are connecting to decide the preference of encryption used. You can always change your browser (Firefox) to make sure that you decide what you are prepared to use as an appropriate cipher in about:config (yes, dragons / warranty etc.). Type in “security.ssl3” without the quotes and turn off everything apart from these (especially MD5 and RC4):
security.ssl3.ecdhe_ecdsa_aes_128_gcm_sha256
security.ssl3.ecdhe_ecdsa_aes_256_sha
security.ssl3.ecdhe_rsa_aes_128_gcm_sha256
security.ssl3.ecdhe_rsa_aes_256_sha
security.ssl3.rsa_aes_256_sha
You can test them at www.SSLlabs.com and www.fortify.net. You should be immune to Logjam, Freak and Poodle vulnerabilities with forward secrecy in most cases.
With Internet Explorer you can change the cipher order by running gpedit.msc and selecting Computer Configuration, Administrative Templates, Network, SSL Configuration Settings. Choose SSL cipher suite order. There is instructions there for editing this. I’m not sure if this works with Edge or how to do this with Chromium based browsers. This certainly gives you a lot more control over how your browsers form secure connections.
Anonymous
I think you misunderstood SLOTH here, it is not related to the cipher algorithm, in which MD5 was known insecure for years, but in the signature algorithm where it was thought to be secure.
You cannot configure which signature algorithm you use in any server/client I have tried (apache, nginx, firefox).
The difference is that ciphering allows for secrecy of the data (you and the server are the only ones who can read the data), while signing allows for accountability and authentication (you know that the data comes from the server).
SLOTH breaks accountability and authentication thus makes man-in-the-middle feasible.
Karthik
Nice article! I am one of the authors of the paper, and I loved this writeup.
Paul Ducklin
Thanks for doing the work and writing the paper (and for your kind words).
We live in a world where website operators regularly lock us out of our accounts due to a password reset following a data breach, causing us to slam up against the inconvenient but temporary brick wall of doing a password reset…
…but we also live in a world where website operators are scared of retiring legacy crypto algorithms or banning tired certificates because it might cause us to slam up against the inconvenient but temporary brick wall of upgrading our browsers for the greater good of all.
Imagine if traffic safety worked that way. “We can’t possibly put a traffic light at this intersection to reduce accidents. Drivers are used to flying down the main road at 100km/hr, and a red light would annoy them.”
Olivia
Very thorough explanation and great article!
Kyle Saia
great article indeed, but what alternatives are there that you could suggest?
Paul Ducklin
Do you mean alternative hash functions? SHA-256 is what most people are using these days.
(There’s also SHA-3 – see the link in the article – which was created with much care and attention to make it deliberately quite different from the earlier SHA algorithms. SHA-1 justifiaby gave crypto experts the same sort of worries as MD5 because it was internally very similar…yet SHA-256 plus its brethren are internally similar to SHA-1, so perhaps the problems with MD5 might apply to the whole lot of them? In other words, why not come up with something that does the same sort of job in very different sort of way? Of course, when SHA-3 was ratified, everyone ignored it. Sucnh is life.)
A casual recommendation – unofficial, unendorsed and probably unqualified – is that if you want hashing algorithms that won’t raise any eyebrows because they re neither too old, nor too new, nor inufficiently “standards-compliant” is as follows:
• For plain hashing, SHA256.
• For keyed hashes, HMAC-SHA-256.
• For converting passwords to “random” hashes: PBKDF2 with HMAC-SHA-256 using 20,000 iterations. (Perhaps double the recommended iteration count every 18 months, say, as computers get faster?)
Dan
I will admit from the outset that I know very little about this subject but from reading the table SHA-1 would require 2 to the 77th power calculations whereas truncated HMAC is 21 magnitudes less secure and is the only security type apart from MD5 which has a measurable time in which it could be broken. How long would a SHA-1 take to break and why is it not secure if the others which have the same level of vulnerability are secure?
Many thanks,
Dan
Paul Ducklin
That’s the point of the article: it’s not a good idea to keep using a cryptographic algorithm once part of its cryptographic promise is broken.
MD5 and its descendant SHA-1 were released under the assertion that they were resilient to all three weaknesses listed above, but they aren’t. But some protocols keep on using them on the very grounds you state, namely, “Why consider it insecure in practice, even if it’s weaker than we thought? It still requires 100 million million million cacluations per connection (277) for a crook to do any harm.”
The SLOTH authors are helping to turn that happy-go-lucky thinking into, “Why consider it secure at all, just because no practical attack yet exists? We already know in theory that it is 10 million million million million (283) times weaker than we thought.”
David Daynard
It doesn’t matter if the “only” attackers with enough processing power are the NSA and perhaps Google if they turned their search engine apparatus to cracking hashes. The point is *someone* has the capability to break it, which automatically makes it insecure.
Mark Stockley
And that’s the best case scenario.
Laurence Marks
Duck wrote:
1. If you deliberately create two messages M1 and M2 such that H(M1) = H(M2), you have a collision, which undermines the value of H as a digital fingerprint. Therefore you should not be able to construct a collision, other than by trying over and over with random inputs until you hit the jackpot by chance.
2. If you know that H(M) = X, but you don’t know M, then you should not be able to “go backwards” from X to M, other than by trying different messages over and over until you hit the jackpot by chance.
3. If you know M, and therefore can compute H(M) = X for yourself, you should not be able to come up with a different message M’ that also has H(M’) = X, other than by guesswork.
Comment 1: Aren’t (1) and (3) the same? They both say you shouldn’t be able to deterministically create two messages with the same hash.
Comment 2: A quibble on the phrase “…trying over and over with random inputs…” Random has a specific meaning: in a random string every digit/bit must have equal probability of occurrence in any of its valid values. I.e., a histogram of a set of random values must be nearly flat. However, in the case of attempting to create a hash collision, there’s no need for randomness. You could attack by trying 1, 2, 3,… or 000, 001, 010, 011,…. As was drummed into my head by a strict Computer Science instructor, one must instead write “…trying over and over again with _arbitrary_ inputs…”
Paul Ducklin
I will edit the text. I have been rather casual in by explanations.
However, the difference between 1 and 3 is that in case 1 *you* are creating two messages – they can be anything you like, so if there is a bias in the hash, for instance, you can choose both of the messages in the same region to improve your chances.
Also, *any* two of the messages in your list can match to hit the jackpot. So every time you choose a new message (e.g via a counter), you win if its hash matches *any* previous message. So your chance that the next message will hit the jackpot gets bigger and bigger every time you compute a new hash. Once you reach just 2N/2 messages in your “pool of potential pairs”, assuming an N-bit hash, your chance of a collision is already about 50:50, and goes steeply up from there. (This is known as the Birthday Paradox, q.v.)
Collisions of this sort generally take the square root of the effort required to find a *specific* hash, which is why this sort of result is usually found first by cryptographers, if a weakness exists.
Case 3 is very different: I fix the first message and you have to find a message with a hash that is the same. This is a slightly stricter version of case 2 (not case 1), where you only need to find a message with a specific hash, whether I already chose a message or not. Case 2 is known as “first pre-image resistance,” because the first match will do. Case 3 is called “second pre-image resistance,” because it means finding a second message of your own that can masquerade as mine.
As for random, you are right. A list of different inputs is simplest. (And won’t repeat until you have tried them all, by which time you will have hit the jackpot, albeit that the universe might be a bit chilly by then.)
Paul Ducklin
See what you think now [2016-01-12T22:34Z].